A Physics Problem, Once Again

Those mating problems in 2D, 3D, 4D and so on, with standard chess pieces adjusted for dimensionality, are extremely difficult and I don’t find a lot about that Googling all around. Perhaps one day, we will have a well-founded theory about that.  Or maybe a solving algorithm for this kind of problems. “How many white kings can hunt down a black horse on a 3D chess board and how?” On the unbounded 3D chess board?

A generalized-chess-mating-SQL.

Perhaps we will have it one day.

Now something to relax. The sum of all gravity forces between each pair of atoms inside our planet Earth. Not as vectors, just the sum of all magnitudes. Approximately.

A discussion there:

http://lesswrong.com/r/discussion/lw/par/open_thread_july_31_august_6_2017/dvy0

 

 

Easier Chess Problem

There is a black queen on the chess board. How many white queens (or how many knights) are needed to take it? No other pieces present, white to move, the black queen is not under attack yet.

Discussion at:

http://lesswrong.com/r/discussion/lw/pa0/open_thread_july_24_july_30_2017/dvo9

Newtonism Question

A mass point of 1 unit is at 1 length unit.

A mass point of 1/2 unit is at 1/10 length unit.

A mass point of 1/4 unit is at 1/100 length unit.

….

Generally, it’s (1/2)^n mass at (1/10) ^n unit for every natural n, on the positive side of 0.

All gravitational net forces point to the left. Where is an opposite reaction force here?

 

 

 

Unexpected?

When you go up the natural numbers ladder, there are (on average) bigger and bigger gaps between consecutive prime numbers.

If you look at primes as islands, there are  lakes of composites between them.

The lake between 19 and 23 is 3 composite numbers long, for example. Or between 89 and 97 there are 7 composites.

Those lakes are greater and greater on average, as it is well known. Albeit there are always small ponds of just 5 composite numbers long, no matter how far you go. (There are likely infinity many lakes with just 1 composite, too. Which is another form of the so called Twin Primes Conjecture. A few years ago it has been proved that there are always less than 70000000 large lakes as you go up the naturals. Some time later, that 70 million has been improved to just 5, but not yet to 1.)

Say, that you have just sailed across some recordly wide composite lake and you are on a prime island again. What can you expect, how much wider will the next record lake be? Usually 2 more composites wider than the previous largest, right?

No. Every new record is usually quite greater from the previous one.

1,2,2,2,6,4,2,2,12,2,8,8,20,14,10,16,2,4,14,16,6,26,30,10,2,12,14,2,32 ...

These are the increments of every new record composite lake.

P.S. Haven’t been able to Google this story.

EDIT:

Then, have been able to Google some about this. The so called maximal prime gap goes like this, says Wikipedia:

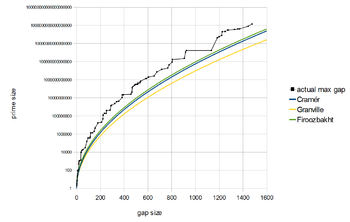
Not as smoothly and gradually as those three coloured functions predict, but quite abruptly in reality.

 

 

 

 

 

 

 

 

 

 

 

4D Mate Problem

Imagine a black chess king  on a 4D chessboard. 8 by 8 by 8 by 8 hypercubes. How many white queens do you need to mate this king, which tries to escape, of course. White doesn’t have a king, just the minimal necessary pack of queens. What is the mating algorithm? Legal moves are analogous to those of 2D chess.

Discussion over there:

http://lesswrong.com/lw/p8a/open_thread_july_10_july_16_2017/dv76

Huffman Codes Problem

Possible, essentially different from each other,  Huffman codes for 5 letters A,B,C,D,E are these 3:

0, 10, 110, 1110, 1111
0, 100, 101, 110, 111
00, 01, 10, 110, 111

 

For all the English alphabet, 26 letters, from A to Z, what are the possible Huffman codes?

EDIT:

Discussion:

http://lesswrong.com/r/discussion/lw/p7c/open_thread_jul_03_jul_09_2017/duwv