Astronomy Problem

What is the per year probability, that we will see a star-star occultation between two non-orbitinging stars, inside our Galaxy?

Discus!

http://lesswrong.com/r/discussion/lw/peg/open_thread_september_11_september_17_2017/dx11

Extremly Easy Problem

Say, that the world sea will actually rise for 6 meters in 100 years.

How many Amazon size rivers do you need on Antarctica on average during all this time?

How many liters of water per second per one meter of Antartica’s shore does this mean?

Chatter:

http://lesswrong.com/r/discussion/lw/pcf/open_thread_august_21_august_27_2017/dweh

Unexpected?

When you go up the natural numbers ladder, there are (on average) bigger and bigger gaps between consecutive prime numbers.

If you look at primes as islands, there are  lakes of composites between them.

The lake between 19 and 23 is 3 composite numbers long, for example. Or between 89 and 97 there are 7 composites.

Those lakes are greater and greater on average, as it is well known. Albeit there are always small ponds of just 5 composite numbers long, no matter how far you go. (There are likely infinity many lakes with just 1 composite, too. Which is another form of the so called Twin Primes Conjecture. A few years ago it has been proved that there are always less than 70000000 large lakes as you go up the naturals. Some time later, that 70 million has been improved to just 5, but not yet to 1.)

Say, that you have just sailed across some recordly wide composite lake and you are on a prime island again. What can you expect, how much wider will the next record lake be? Usually 2 more composites wider than the previous largest, right?

No. Every new record is usually quite greater from the previous one.

1,2,2,2,6,4,2,2,12,2,8,8,20,14,10,16,2,4,14,16,6,26,30,10,2,12,14,2,32 ...

These are the increments of every new record composite lake.

P.S. Haven’t been able to Google this story.

EDIT:

Then, have been able to Google some about this. The so called maximal prime gap goes like this, says Wikipedia:

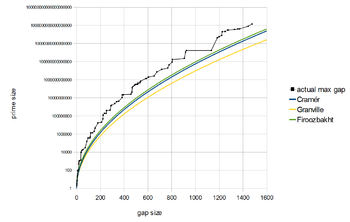
Not as smoothly and gradually as those three coloured functions predict, but quite abruptly in reality.

 

 

 

 

 

 

 

 

 

 

 

Set Theory Problem

There are at most aleph-zero disjunct 3D spheres in 3D space. And there are at least aleph-one disjunct 2D circles in every finite volume part of the 3D space?

The number of points in N dimensional space is always aleph-one. And you can also divide this space into aleph-one disjunct N-1 dimensional spheres.

Is there a way to divide 3D space into aleph-one cubes with no common volume? They may touch each other, but may not share some common volume.

If you can find one such space division, you brought down the ZF Set Theory.

EDIT:

Discussion there:

http://lesswrong.com/lw/p5p/open_thread_june_19_june_25_2017/du4t

Alpha-Primes Problem

Which minimal length English sentence describes the set of all  primes smaller than 100?

You can use numerals as well.

 

Another Intermezzo Intermezzo Problem

The first one was solved by Oscar Cunningham and the point of the solution is that every probable black hole lasts for at least a million years longer, if you add just one hydrogen atom into it. Of course, a supermassive black hole acquires even much longer additional time with every hydrogen atom acquisition, or shall we say — a merger with a single hydrogen atom.

It is reasonable to assume, that our domestic SMBH’s lifespan is prolonged by 10^60+ years per second, due the regular infall. Assuming also, that there will be no Big Rip or something equally unpleasant for black holes in the future.

While we still don’t know the definite answer to the Intermezzo problem, here is another inter-intermezzo.

Are there non synthesizable molecules, which would be stable if they somehow managed to pop up into existence by magic or by some weird quantum fluctuation? (Non-synthesizable-repeatedly from chemistry/physics/mathematics/logic reasons.)

 

 

 

 

 

 

 

Intermezzo Problem Solution(s)

Below there is a problem I invented a month or so ago. I published a link on Lesswrong and the solving began.

The first solution was 4 hexagons by LW user 9eB1. He later improved it by, quote:

 right triangle that’s half the area of the equilateral triangle. You can fit 4 in the square and two in the triangle, and the score is point six

Oscar Cunningham came with this, quote:

why not get a really good score by taking a completely gigantic shape that doesn’t cover anything

This is a clever but also somehow trivial solution, we have agreed.

So he came with thi:

The thin red line is the uncovered area of the square, while the triangle can be tiled perfectly. The score is 0.57756.

Then I made I little promise, which has been broken already, that I will publish my solution on Monday, which is about two weeks ago by now.

The whole time, I was digitally evolving solutions on a computer. Just as I was not very far from Oscar’s solution he stroke again, with a much better one. More than twice as good as the previous one. This time he perfectly tiled the square and left some triangle uncovered. The score is 0.249..

This morning I almost decided to quit, when I saw something unusual on the screen. At first, I thought something wasn’t right. Then I realized what the damn computer is telling me.

The computer was evolving the following picture (visually rephrased by me for clearness).

The perfect score 0, albeit a bit trivial solution perhaps. Of course it is not necessary that you join the triangle and the square together. You can split the covering shape. Which computer did.

EDIT: 

The problem is with the Oscar’s last solution. When I put his algorithm into the machine, it showed an error in the form of a negative result.

Well, the algorithm is okay, but 1/7 and 1/4 can’t be. But 1/7 and 1/12 can be. But the result isn’t that good.

Intermezzo Problem

We have the unit (edge length equal 1)  square and the unit edge equilateral  triangle.

Choose a shape, such that many instances of that shape (maybe flipped or rotated) tile both polygons. There must be no overlaps and no part of the covering shape may lie outside both polygons.

A shape that leaves a smaller percentage of its own area uncovered is a better solution.

Which shape is the best covering solution?

Landau’s Problem, Continuation

In fact, the only possible prime divisors of numbers that are equal to N*N+1, are the members of the sequence A002313.

Those are: 2, 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101 …

The number 2, as a divisor, covers 1/2 of them all. The number 5 covers 2/5 of those already covered by 2 and also 2/5 of those not divisible by 2. The number 13 covers 2/13 of them, and so on. Every prime P from this sequence, except for 2,  covers (as a divisor) 2/P of all increased squares.

The infinite product (1/2)*(3/5)*(11/13)*(15/17)*(27/29)… tells us what percentage of N*N+1 numbers are primes.

If this infinite product converges to 0, which is to say that it diverges, which is the usual convention when we deal with infinite products … then the Landau’s problem isn’t solved. There may be a finite or an infinite number of primes which are squares increased by 1.

However, if this infinite product converges to something greater  than 0, then Landau’s problem is solved and there are an infinite number of such primes. It is expected, that there actually are such primes all the way up. A positive percentage isn’t expected. That would be yooge!

Just prove the convergence of said infinite product! How hard could it be?

 

 

 

 

More on Landau’s Problem

If there is a natural P, such that there is no prime of the form N*N+1 above P, then we have the following situation:

Every square number N*N, greater than P, is congruent with some smaller square number M*M, modulo Q; residium Q-1. Where Q divides some J*J+1 and J is smaller or equal M.

For example, 13*13+1=170=2*5*17. 2 and 5 are smaller than 13 and they both need to be divisors of some smaller square number plus 1. 17 is also 4*4+1, but since it is greater than 13, it need not to be a divisor of a smaller square plus 1. It may.

For 11*11+1=122=2*61, 2 is a divisor of 1*1+1=2, but 61 is a first timer. It divides many bigger squares plus 1. Every I*I+1, where I is K*61+11 or K*61+50. Notice that 50+11=61, and this is not a coincidence, either.

For example, 9*9+1=82=2*41. 41 is the first timer here, but it divides 32*32+1=1025=5*5*41. And every I*I+1, where I is K*41+9 or K*41+32. See, 32+9=41.

The smallest nontrivial divisor of squares plus 1, which is 2, divides I*I+1 whenever I is of the form K*1+1 or K*1+1 (which are the same) and 1+1=2.

And the next nontrivial divisor of squares plus 1, which is 5,  divides all I*I+1, where I is of the form K*2+2 or K*2+3 (the same thing (only) here) and 2+3=5.

Squares plus 1, have a special sequence of divisors: 2, 5, 10, 13, 17, 25, 26, 29, 34, 37, 41, 50, 53, 58, 61 … (Sloane A008784)

(We can prove all of that, but it’s off topic for the moment.)

Knowing all of this, one has to prove only, that there are always squares, such they are not congruent to a smaller square, modulo one of these numbers, residue that number minus 1.

In other words, do you think, that above some number, all the squares are congruent to smaller squares by a member of this sequence, residue this number minus 1?